黑盒理论与贝尔不等式 (I)
EPR paper
在我开始讨论贝尔不等式之前, 我想先明确一下 EPR 问题. EPR 问题是现代物理从经典理论推广到量子理论的必要性的核心. EPR paper 论证的核心在于, 量子理论的:
- 完备性, 即量子理论可以描述所有的自然态与过程.
- (演化的)局域性, 物态的演化只与局域性质有关, 某一点下一刻的性质仅取决于该点当前的性质.
- (物理)实在性, 物态可以由可观测量完全描述, 可观测量是物体的本征属性, 与是否被测量无关.
三者不全为真.
爱因斯坦 (代表了上世纪初, 甚至可以说自牛顿以来绝大多数物理学家的信仰) 坚信物理实在性必然是真的. 而上世纪初大家基本都认同了狭义相对论的正确性, 也即是局域性的正确性. 因而爱因斯坦总结到
“量子理论必然是不完备的”.
但是贝尔实验的出现冲击了所有物理学家的世界观, 这个实验证明了局域性与实在性本身就是矛盾的, 我们必须抛弃其中之一. 当然, 贝尔实验, 或者说黑盒模型默认了一个前提: 自由意志. 但是如果我们放弃自由意志的假设, 我们对物理的讨论将不可避免的倒向本体论, 变得过于复杂.
与很多人想象的不一样, 我们现在普遍接受的量子理论是局域非实在的. 也就是我们抛弃了实在性假设, 保留了局域性 (这里的局域性指的是演化的局域性, 而我们说的量子非局域指的是态的描述的局域性). 本文承接前文的框架来介绍一下贝尔不等式及其揭示的本质, 并且让大家更深入的理解一下什么是局域性与实在性. 在现代量子信息学中, 贝尔不等式并不算一个非常好的不等式 (当然, 从实验的角度来说, 这个是最简单模型), 但是它是第一个揭示出现实与经典理论相悖这个事实的理论.
实在理论
在量子信息初探 - 态, 测量与信道中我们说到, 我们对自然所有的认知都来源于制备初态 $\rho$, 然后进行测量 $M=\qty{E_1,E_2,\cdots,E_m}$. 其中测量的概率是由一个内积 $\braket{E_i}{\rho}$ 给出的. 一个测量的集合与态一起给出了测量结果的概率分布, 而可观察量就是这个概率分布上的随机变量. 经典理论与量子理论的核心差别就是这个内积的结构. 对经典理论, 这个内积是向量的(复)欧几里得内积, 也就是向量点乘 $\vec{E_i}^\ast\cdot\vec{v}$. 而量子理论使用的内积是复希尔伯特空间上的有界半正定算子内积, 或者说 Hilbert-Schimidt 内积 $\tr(E_i^\dagger \rho)$.
根据概率的定义, 我们有 $\braket{E_i}{\rho}\geq 0$ 与 $\sum_i\braket{E_i}{\rho}= 1$ 的限制. 如果加上对于每一个 $E_i$ 都存在 $\rho_i$ 使得 $\braket{E_i}{\rho_i}=1$, 则经典理论中测量是一组标准正交基. 这个标准正交基是唯一确定的, 否则必然存在某些态在某些测量下会出现负概率. 但是对于量子理论, 我们只需要保证态 $\rho\geq 0$ 是迹为 $1$ 的半正定算子, 而 $E_i\geq 0$ 是半正定算子并且 $\sum_i E_i =\mathbb{I}$. 对于本征态存在性的假设, 我们只需要使得测量为完备正交投影算子集合. 同一个空间中可以有多种测量基存在.
经典理论中测量的唯一性就揭示了, 一组完备测量基底对应的态完整的描述了态 $\rho$, 因为不存在同一空间中的另一组基去区分拥有相同可观测量的两个态. 但是在量子理论中, 非对易的两个测量是可以区分拥有相同可观测量的两个态的, 用可观测量来描述态是不完备的.
简单起见, 我们举一个例子.
- 粒子自旋
-
我们可以测量粒子在 $z$ 方向的自旋. 假设这个测量的结果是离散的 (正如我们在实验中测到的那样), 自旋可以是上或者下. 如果一个态在测量后总是给出自旋上, 我们把这个态叫 $\uparrow$, 如果总是自旋下, 这个态就叫 $\downarrow$. 对于这样的二元测量, 结果总是可以用向上自旋的概率 $p$ 来表示. 我们把自旋上概率为 $p$ 的态写做 $p\ketbra{\uparrow}{\uparrow}+(1-p)\ketbra{\downarrow}{\downarrow}$ 或者 $\binom{p}{1-p}$. 在经典理论中, 我们认为物质就是可观测量的集合, 概率的本质是源的概率. $\binom{p}{1-p}$ 这样的态本质上是从源中以概率 $p$ 给出一个态 $\outter{\uparrow}{\uparrow}$. 只有给出确定性测量结果的态才是真实的. 我们把这样的理论叫做物理实在的. 这样的经典态是被一个固定的测量唯一确定的. 也就是这个态可以用测量统计来描述的, 拥有相同测量统计的两个态是不可区分的:
\begin{equation} \begin{aligned} \rho & \equiv \braket{\vec{E}_1}{\vec{\rho}}\vec{E}_1+ \braket{\vec{E}_2}{\vec{\rho}}\vec{E}_2 \\
& =\qty[(1,0)\pmqty{p\\ 1-p}] \pmqty{1\\ 0} +\qty[(0,1)\pmqty{p\\ 1-p}]\pmqty{0\\ 1} \end{aligned} \end{equation}但是在量子理论中, 我们发现测量统计不足以描述所有的量子态, 我们的量子态应该由半正定算子描述:
\begin{equation} \rho=\pmqty{p&a\\ a^\dagger&1-p} \end{equation}
其中 $\norm{a}^2 \leq 4p(1-p)$. 对于投影算子 $ E_1=\pmqty{ 1&0\\0&0}; E_2=\pmqty{ 0&0\\0&1}$, 测量统计并不能还原态所有的信息:
\begin{equation} \braket{E_1}{\rho}E_1+ \braket{E_2}{\rho}E_2 = \pmqty{p&0\\0&1-p} \neq\rho \ . \end{equation}
贝尔不等式的意义就在于, 告诉了我们这个拓展是必要的 (除非我们接受非局域隐变量).
局域性
在量子信息学中, 我们不关心物态具体如何演化的, 我们说的局域性比物理的局域性更加广义. 在物理上, 我们说局域性一般指狭义相对论语境下的局域性. 这类局域性假设场的连续性. 我们假设场是一个关于时间与空间的函数: $V(\vec r,t)$. 当然, 这个”场”包含了我们需要描述物态的所有性质, 比如 电磁场, 质量密度, 电荷密度等等. 局域性的意思就是 $\dv{t} V(\vec{r},t) = f\qty(V(\vec{r},t))$, 其中 $f$ 可以包含任意阶的偏导. 也就是场在 $t$ 时刻, $\vec{r}$ 位置的演化是由该场在 $t$ 时刻, $\vec{r}$ 位置的性质(包括各阶导数)唯一确定的. 与该场其他时刻, 其他位置的性质 $V(\vec{r}^\prime,t^\prime)$ 无关.
在量子信息中, 我们对局域性考察的是两个类空事件的相关性. 理论上我们不关心两个事件是否是类空的, 我们只关心两个事件的相关性. 在实验上, 我们假设侠义相对论是对的. 只要实验时我们在遥远的两个地方进行实验, 它们发生的间隔不足以让光从一方跑到另一方, 我们就认为它们之间是类空的. 根据信息学的习惯, 我们把事件发生的两个地点叫做 Alice 与 Bob (如果有第三方就叫 Charlie, 或者在密码学中窃听方一般叫 Evil).
让我们暂且丢掉对态的描述, 仅从概率论的角度来讨论一下测量统计, 这便是黑盒模型.
假设 Alice 与 Bob 共享了一个态. 我们不关心这个态从何而来, 我们对这个态也一无所知, 甚至不知道 Bob 是不是真的得到了部分的态. 我们只知道 Alice 与 Bob 可以对它们进行测量. Alice 可以任意从一个测量的集合 $\qty{A_1,\cdots}$ 中选择一个测量 $A_i$. 我们可以用字母表 $X$ 标记每个测量的结果 $a\in X$. 同样的我们可以对 Bob 定义测量集合 $\qty{B_1,\cdots}$ 以及字母表 $Y=\qty{b}$.
这样, 给定两个测量 $A,B$, 我们可以得到一个实验统计 $P(a,b\vert A,B)$. 假设 Alice 与 Bob 进行测量是类空事件, 也就是它们没有因果关系, 那么必然有
\[\begin{equation} \begin{aligned} \sum_{b} \prob{a,b\vert A,B} &= \sum_{b} \prob{a,b\vert A,B^\prime} \\ \sum_{a} \prob{a,b\vert A,B} &= \sum_{a} \prob{a,b\vert A^\prime,B} \end{aligned} \end{equation}\]也就是说, $P(a\vert A,B)$ 与测量 $B$ 的选择无关, $P(b\vert A,B)$ 与 $A$ 的选择也无关. 如果在某个实验中, 这一点被违背了, 那么就证明了这两个事件有因果关系 (非条件独立). 如果这两个事件距离大于光速, 但是却是非类空的, 这证明侠义相对论是错的. 我们从来没有观测到过这样的实验结果.
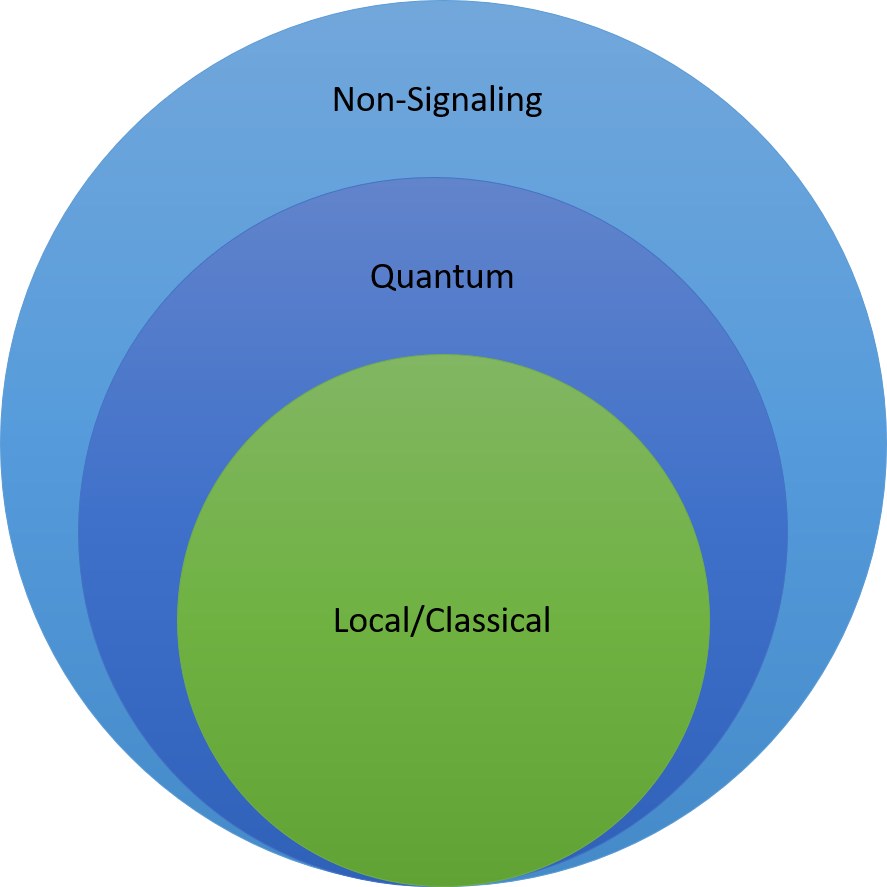
在量子信息中, 满足这个等式的理论叫做”无信号理论” (non-signaling), 满足量子关联(由 Hilbert-Schmidt 内积描述)的理论叫做”量子理论” (quantum), 满足经典关联(由欧几里得内积描述)的理论叫做”局域理论” (local). 不过我不是很喜欢 local 这个名字, 它与狭义相对论定义的 local 是不同的东西, 最好还是叫”局域实在理论” (local realistic).
黑盒理论与贝尔不等式 (II)中我会展示一下 $\text{local}\subsetneq\text{quantum}\subsetneq\text{non-signaling}$, 以及 Bell 不等式, 或者说 CHSH 不等式.