量子信息基础 - 态, 测量与信道
本章主要目的是介绍物理系统的必然形式, 半严格地推导出一切物理图像的必要结构. 根据目前的实验结果, 当前量子理论的结构是充分必要的. 量子信息论讨论的便是量子理论结构的数学形式. 从数学上说
量子信息论就是一门关于(有限维)单位迹半正定算子 $\rho$ 以及 CPTP 超算子 $\Phi$ 的学科.
人类如何认知自然
在我们任何物理问题之前, 让我们首先思考一下人类是如何认知自然的. 哪些信息是我们客观得到的, 哪些是我们幻想出来的呢?
我本科的时候老师说的一句话我至今记忆犹新. 物理学到底是什么呢?
物理学的本质就是描述, 并且预测自然.
但是我们对物理系统的描述与预测并不是空想出来的. 相信很多人在中小学的时候都常常听到这样一句话,
物理是一门实验科学.
我们一切对物理系统的描述与预测都应当是基于实验结果的. “实验”包含了我们在实验室里做的真正的科学实验, 但同时包含了人类在日常生活中进行的一切体验. 我们所有对自然过程的描述都必须与实验相一致, 而我们所有对自然的预测的正确性都是由实验统计与概率论来保证的. 所以, 如何理解”实验”是讨论一切物理理论的关键. 量子世界的诡异性质逼迫我们对”实验”的细节进行更深入的思考, 因而催生出了一般概率性理论 (GPT, generalized probabilistic theory):
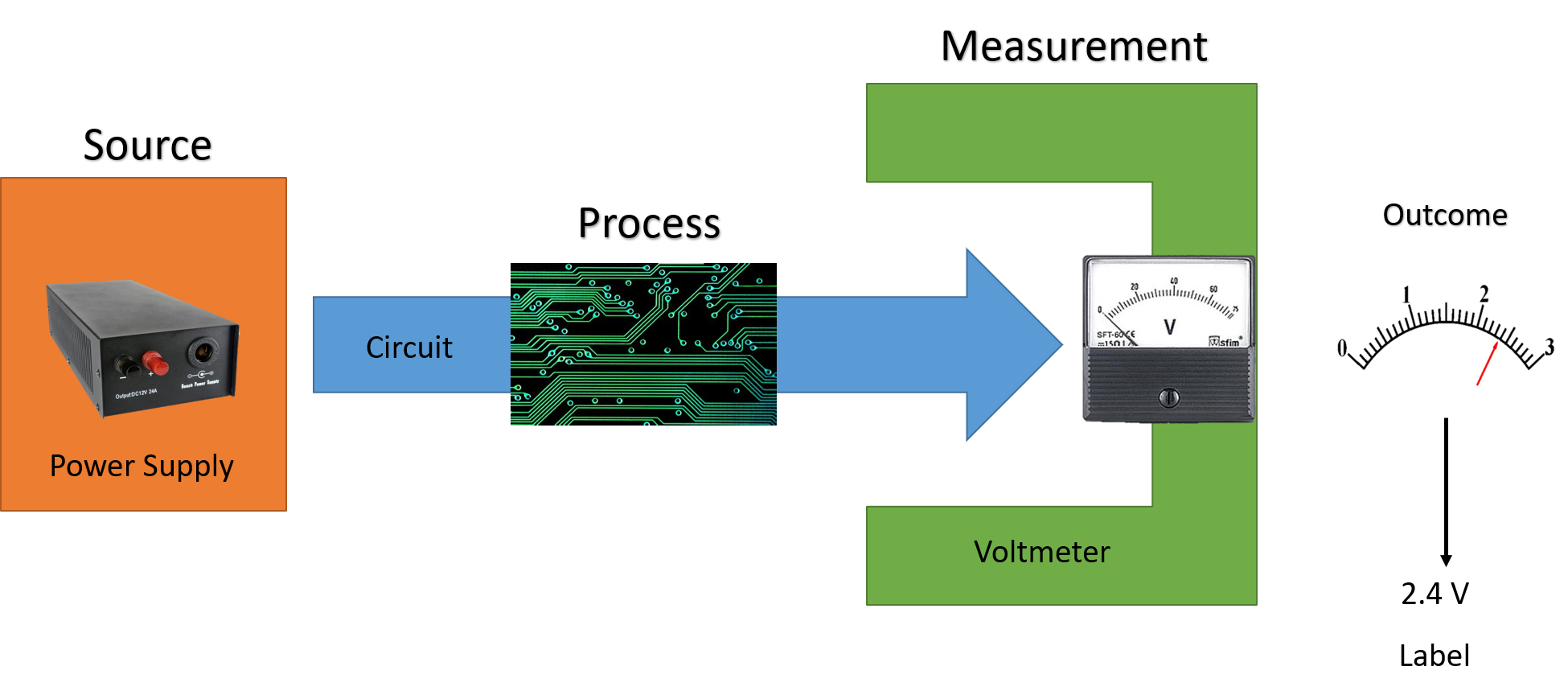
一般概率性理论是关于描述一切实验的理论. 当然, 可以囊括一切并不代表它是一个完美的理论. 一个好的理论不止需要有能力描述一切的现象, 还需要有能力预言更多的事件. 不同于传统上大家在物理系统中一点一点构造出逼近实验的理论框架, 在一般概率性理论中, 我们实际上是先写下一切的可能理论, 然后一步一步加上限制条件, 从而逼近实验的结果. 在一般概率性理论中, 一切实验都被分为了三部分:
- 源 (Source)
-
源确定了实验系统的初态. 在一般实验(特别是经典物理实验)中, 初态可以是一个确定的状态, 也即”源”可以不断的提供一个确定的初态. 然而这一点在现实的实验中是很难完成的. 实验中总是有不确定因素存在, 因而源的状态必然会受到或多或少的未知扰动. 既然我们无法知道这些扰动的信息, 自然我们也无法验证”源”所提供的初态到底是什么. 但是我们可以知道”源”的统计. 在这种情况下, 实验的”源”是由一个概率分布来描述的. 我们可以把源 $S$ 看作一个 $(\rho_i,p_i)$ 的系综, 它以一定的概率生成一个状态(态) $\rho_i$.
- 过程 (Process)
-
正如其字面意思, 过程 $P$ 是一个自然过程, 也即是物理实验的关键. “过程”本身与我们是隔离开的. 一切关于”过程”的信息我们都只能通过”源”与”测量”来获得. 当我们研究物理的时候, 事实上我们想刻画的便是这个”过程”.
- 测量 (Measurement)
-
测量便是我们从自然过程中提取信息的步骤. 通过测量, 我们可以得到一次实验的结果. 通过不断的实验, 我们可以得到该实验的一个统计. 也就是说, 测量 $M$ 会给出测量结果 $(E_k, p_k)$, 即以一定概率 $p_k$ 得到结果 $E_k$. 这个 $E_k$ 常常被称为测量的效应 (Effect).
对我们人类而言, 源 $S$ 与测量 $M$ 的统计就是自然过程的一个描述. 如果两个物理过程中对于所有可能的 $(S,M)$ 的统计完全相同, 则这两个过程是不可区分的. 倘若我们接受概率论, 则我们可以说物理过程是由所有 $(S,M)$ 的概率分布唯一确定的. 当然, 从实验的角度而言, 我们可以获得的信息其实是由 $(S,P,M)$ 共同组成的. 也即是说, 我们能够从实验中获得的数据有且仅有条件概率 $\prob{E_k\vert S,P,M}$.
如果一只鸟走起来像鸭子、游泳起来像鸭子、叫起来也像鸭子,那么它就是鸭子
测量与态
注意, 我们一切的实验的结果最终都是由测量所给出. 测量的本质便是从一个源 $S$ 中提取经典信息. 过程 $P$ 总是可以被看作源或者测量的一部分, 因而我们可以先将其隐藏起来. 将测量 $M$ 所有可能的结果的集合 $\qty{E_k}$ 记为一个样本空间 $\Omega_M$. 在量子信息论中, 我们常常假设 $\Omega_M$ 是有限的, 但是很多时候我们的结论对无穷大样本空间也适用. 在这里, 我们也暂且假设它有限, 这样我们在定义各个概念的时候可以省去对存在性的讨论. 因此在讨论概率的时候, 我们这里使用求和而不是积分.
所谓的提取信息便是, 对于一个给定的源 $S$, 输出 $\Omega_M$ 中的一个结果. 这个输出可以是确定性的, 也可以是概率性的. 如果我们的源与测量都是良定义的, 则一对 $(S,M)$ 定义了 $\Omega_M$ 上的一个概率分布 $\mathcal{D}$. 我们物理上说的可观测量 (observable) 实际上就是 $\Omega_M$ 上的(实)随机变量. 在经典物理中, 倘若 $(S,M)$ 不能给出一个确定性的输出, 我们总是假设这个概率分布来自于 $S$ 本身 (物理系统的实在性). 即 $S = (\rho_i, p_i)$, 就是 $S$ 以 $p_i$ 的概率输出态 $\rho_i$. 其中, 在测量 $M$ 下, $\rho_i$ 总是确定性地给出一个结果 $E_i \in \Omega_M$.
在物理上, 我们总是将可观测量的均值当作其真实值. 譬如我们测量一个电路上两点的电压时, 由于各类的噪声, 测量的结果总是会有一定的波动. 在实验上, 我们便将平均数据作为测量的结果, 将波动的范围作为误差. 给定一个 $\Omega_M$ 上的随机变量 $f_M$, 其均值 $\ev{f}_M$ 由 $\sum_k \prob{E_k\vert S,M}\cdot f_M(E_k)$ 给出. 由于我们的源以 $p_i$ 的概率输出 $\rho_i$, 我们有 $\prob{E_k\vert S,M} = \sum_i \prob{E_k\vert \rho_i, M} p_i$. 因此我们有 \begin{equation}\label{eq:observable} \ev{f}_M = \sum_i \sum_k \prob{E_k\vert\rho_i,M} p_i \cdot f_M(E_k) \ . \end{equation} 这也可以推广到 $f_M$ 的任意阶矩 $\ev{f^n}_M$.
我们选择将 $\rho_i$ 嵌入到一个实线性空间 $V_M$ 中. 然后我们可以将源 $S$ 写做凸组合 $\ket{\rho}_M = \sum_i p_i \ket{\rho_i}_M$. 注意, 这个空间可以是依赖于测量 $M$ 的.
$\sum_ip_i=1, p_i\geq 0$, 它们构成一个概率向量 $(p_1,p_2\cdots,p_m)$. 这个概率向量定义的线性组合 $\rho=\sum_i p_i\rho_i$ 被叫做凸组合.
我们再把 $E_k$ 看作对偶空间 $V^\ast_M$ 中的元素, 使得 $\prob{E_k\vert \rho_i,M} = \braket{E_k}{\rho_i}_M$. 那么 $\prob{E_k \vert \rho, M} = \sum_i p_i \braket{E_k}{\rho_i}_M = \braket{E_k}{\rho}_M$. 可观测量即可被写做 \begin{equation} \ev{f}_M = \sum_k \braket{E_k}{\rho}_M f_M(E_k) \ . \end{equation} 根据均值的定义, 不难证明如上代数结构满足线性空间的定义.
- 注意
-
这个式子与 \eqref{eq:observable} 是等价的. 我们只是用线性代数的语言重述了原来由概率论语言给出的描述.
由于条件概率, 或者说可观测量是我们仅有的对系统的认知, 因而我们只可能从系统中获取 $\rho$, 而非 $(\rho_i, p_i)$ 的信息. 当 $\rho_i, M$ 总是给出一个确定性的结果 $E_i$ 时, $\sum_k \prob{E_k\vert\rho_i}f_M(E_k) = f_M(E_i)$, 也就是说 \begin{equation} \ev{f}_M = \sum_i p_i f_M(E_i) \ . \end{equation}
需要注意的是, 我们如上对可观测量的描述都带有测量 $M$ 的下标. 也就是说, 我们考虑了可观测量在不同测量下有不同定义的可能性. 这样的性质被称为互文. 但是我们天然的直觉告诉我们, 一个系统本身蕴含的信息不应该与我们如何测量它相关. 也就是说, 对任意两个测量 $M,M^\prime$, 如果他们共享一部分的测量效应, 那么对任意两个以 $M\cap M^\prime$ 为支撑集的可观测量, $f_M = f_{M^\prime}$. 在这种情况下, 我们可以简单的去掉下标 $M$, 即 $\ev{f}_M = \ev{f}$. 然而贝尔实验告诉我们, 存在 4 组测量, $\qty{M_1,M_2,M_3,M_4}$ 上的可观测量 $\qty{f_1,f_2,f_3,f_4}$ (假设我们的世界是定域性的), 不可能有可共存 (compatible) 的分解 \begin{equation} \ev{f} = \sum_i p_i f(E_i) \ . \end{equation} 这一点可以在黑盒模型上利用 CHSH 不等式证明, 参见黑盒理论与贝尔不等式 (I).
- 事实
-
贝尔实验的结果意味着, $\rho_i$ 的凸组合并不足以描述所有可能的态. 也就是说我们不能仅仅用测量的结果 $E_k$, 譬如位置, 动量, 角动量等等的测量值来唯一地确定一个物理系统的状态, 即一般而言 $\ket{\rho} \neq \sum_k\braket{E_k}{\rho}\ket{\rho_k}$. 测量的概率必须是由 $(\rho,M)$ 共同决定的.
为了了解如何才能描述 $\rho$, 我们必须确定先考察 $E$ 与 $\rho$ 需要满足的必然条件. 首先, 显然存在一个平凡测量, 其对所有输入给出唯一确定的结果. 我们可以将其写做 $\bra{\id}$, 使得 $\braket{\id}{\rho} = 1$. 其次, 因为对于所有输入, 我们总可以有一个可能的结果 $E_i$, 这些结果的概率之和永远为 $1$. 如果我们遗忘掉所有的结果, 那么这个测量等同于输出固定结果的测量, 即 $\sum_k \bra{E_k}=\bra{\mathbb{I}}$. 另外, 由于 $\braket{E}{\rho}$ 描述的是一个概率分布, 其必然大于 $0$.
综上所述
- 对所有可能的态 $\rho$ 都有 $\braket{\id}{\rho} = 1$.
- 对于一个给定的测量 $M$, 它的所有可能的输出 $\sum_k \bra{E_k} = \bra{\id}$.
- 对所有可能的态 $\rho$ 与测量结果 $E_k$, $\braket{E_k}{\rho} \geq 0$.
但是注意, 正如我们前面所说, 一般而言 $\rho\neq \sum_i\braket{E_i}{\rho}\ket{E_i}$. 这个内积绝不是常见的欧几里得内积.
- 在欧几里得内积下
-
- $\braket{\mathbb{I}}{\rho} = 1 \Rightarrow \norm{\rho}_1 = 1$.
- $\sum_k \bra{E_k} = \bra{\id} \Rightarrow \sum_k \bra{E_k} = (1,\dots,1)$, 即所有元素都是 $1$ 的(对偶)向量.
- $\braket{E_k}{\rho}\geq 0 \Rightarrow$ $\rho$ 为概率向量, $E_k$ 的所有元素都非负.
在量子物理中, 我们知道这个内积是有界算子的内积 (Hilbert-Schmidt 内积) $\braket{A}{B} := \tr (B^\dagger A)$. (算子内积在对角算子上会退化为欧几里得内积, 也就是可以退化为经典物理.) 这是对自然系统描述的已知最简形式. 正如对相对论力学可以退化为牛顿力学, 即便量子理论有所欠缺, 新的理论也必须能退化成这个算子内积的形式.
- 在算子内积下
-
- $\braket{\mathbb{I}}{\rho} = 1 \Rightarrow \tr(\rho) = 1$.
- $\sum_k \bra{E_k} = \bra{\id} \Rightarrow \sum_k E_k = \id$
- $\braket{E_k}{\rho}\geq 0 \Rightarrow E_k\geq 0, \rho\geq 0$. (算子 $A\geq 0$ 的意思是 $A$ 是半正定的).
我们现在就得到了量子信息的基础结构: 所有物理态都是由迹为 1 的半正定算子所描述的.
注意, 我前面讨论的问题极其基本, 我甚至没有讨论一个态被测量后会变成什么, 以及态如何演化.
信道
Information is physical
我们对物理系统的讨论的本质是从测量中提取的信息. 但事实上物理本质上就是信息, 或者说人类对物理系统的一切认知本质上就是信息. 这也是为什么我们虽然在讨论物理的本质问题, 这个方向却叫”信息论”. 我们将一切的物理状态都看作信源, 则物理状态的变化本质上就是信源的变化. 我们借用经典信息论的语言, 把一切态的转化叫做量子信道.
基于概率叠加的线性结构, 量子信道应当是从有界算子到有界算子的映射, 或者叫超算子. 一个物理系统在变化之后必然还是一个物理系统, 那么量子信道必然要保持量子态的性质:
- $\tr(\rho) = 1$.
- $\rho\geq 0$
对于第一点, 我们要保证信道 $\Phi$ 作用在迹为 1 的态 $\rho$ 上后, $\tr(\Phi(\rho))=1$. 同时因为线性, 这等价于 $\tr(\rho) = \tr(\Phi(\rho))$. 这样的超算子叫做保迹映射 (trace preserving, 缩写为 TP).
对于第二点, 我们要保证对于所有的半正定算子 $\rho\geq 0\Rightarrow \Phi(\rho)\geq0$. 这样的超算子叫做正映射. 但是正映射有一个很麻烦的问题. 如果我们将 $\rho$ 看做一个大系统上的子系统, 也就是说它代表着大系统中的某些独立自由度. 在数学上这意味着它是大空间 $\hilb^{AB}$ 中的一个子空间 $\hilb^B$ 上的算子. 然而对于所有半正定算子 $\tilde{\rho}\in\hilb^{AB}$, 即使 $\Phi$ 是正映射, $\id_A\otimes\Phi(\tilde{\rho})$ 却不一定是半正定算子. 也就是说, 即使是在子系统中看似可以将一个态映射到另一个态上的超算子也可能在大空间上把一个态映射到不合法的算子上. 设 $A$ 系统的维度为 $n$, 则我们把拓展后还是正映射的算子叫做 $n$-正映射. 如果对于所有 $n\geq 0$, $\mathbb{I}_n\otimes\Phi$ 都是正的, 我们则说 $\Phi$ 是全正映射 (complete-positive, 缩写为 CP). 实际上, 可以证明, 当 $n$ 大于 $B$ 系统的维度的时候, 就已经可以保证这个映射是全正的了.
在量子信息论中, 我们定义量子信道为所有的 CPTP 超映射.
简单的说, 量子信息论就是一门关于(有限维)单位迹半正定算子 $\rho$ 以及 CPTP 超算子 $\Phi$ 的学科.