信息的度量
在之前的文章中, 我讨论了量子过程的数学结构与张量表示. 然而这些只是讨论量子信息时候必要的数学工具, 而非量子信息本身. 对量子信息而言, 我们应该关注的是量子数据与量子信息处理, 而非线性代数的抽象结构. 为了讨论这一点, 我们需要在量子态与量子信道的基础上加入信息论的度量.
量子信息不同于量子计算的一点在于, 量子信息是基底变换不变的. 在经典信息论中, 如果一个信道仅仅将信号 $a$ 与信号 $b$ 进行交换, 经过它的信息量并不会出现任何损失. 因为只要我们知道该信道的全部性质, 我们就可以在接收端进行一个局域的操作, 完美还原出源信号. 但是在计算中, 输出 $0$ 与输出 $1$ 是截然不同的结果. 我们必须严格区分输出的状态, 因为类似信道中的后处理过程也必须算作量子计算的一部分.
信息与信息处理
在信息论中, 信息是一种重构历史的能力. 比如你用电脑画一张画发给朋友. 这张画会被转换成一串由 $0$, $1$ 组成的数据流, 然后通过一系列网络传输协议到达你朋友的电脑上. 你朋友的电脑可以通过收到的数据流重构出你的图片, 显示在显示器上. 也就是说, 通过信道 (即从你按下发送键到你朋友显示器上出现图片这中间发生的整个过程) 你的朋友可以在几秒钟后知道你几秒钟之前看到了什么. 然而由于网络不是稳定的, 这个信息传输的过程中可能会发生丢包. 假设你的电脑不会重复发送同样的数据, 那么你朋友只能收到部分的数据, 然后通过这部分数据去猜你原来传输了什么. 随着丢包的数量上升, 你朋友电脑重构出来的图片会失真的越来越离谱. 在互联网早期常见的图片绿色包浆就是这种信息丢失的一种著名的例子.
在信息论中, 这种信息损失过程叫做
- 数据处理不等式
-
在信息的传递过程中, 信息量只会不断的损失而无法被恢复.
在经典信息论中, 数据处理不等式通常由互信息 $I$ 所表述: 在信息从 $X$ 到 $Z$ 的传递过程中
\[X\to Y\to Z\]我们有 $I(X,Y) \geq I(X,Z)$. 即 $Z$ 系统得到的信息还原出的 $X$ 系统中的源信息一定不可能比中间系统 $Y$ 还原的更好.
我们暂且不讨论互信息 $I$ 是如何定义的. 这里首先需要明晰信息论中的系统 $X,Y$ 与 $Z$ 是什么. 一个很重要的概念是, 信息论讨论的并不是某次具体的传输过程发生了什么, 而是同一个信号处理过程在无数次使用中的整体性质. 因此, 为了定义一个系统, 我们首先要列出这个系统所有可能出现的状态集合 $\Gamma_X, \Gamma_Y$ 与 $\Gamma_Z$. 他们表示的可以是一些物理状态的集合, 但是在理论处理过程中, 我们应该把它们理解成字母表. 其中每个字母表中的符号都指代了一个或多个物理状态. 简单起见, 可以将它们理解为在电路中用符号 $h$ 代表高电平, 用符号 $l$ 代表低电平. 电路中的电平可能有扰动, 因而电压状态可以是无穷多的. 但是我们关心的只有 $h$ 与 $l$ 两种状态, 因而我们在信息论中不需要考虑具体的电平是多少.
在对一个信息处理过程无数次的使用中, 它并不是完美的将信号传递出去的. 这个过程中可能会有随机的扰动. 即使是一个确定的信息源给出的固定的信号, 在传播出去后也有可能出现随机的变化. 因此我们需要用概率来描述一个信号在传递的不同中间系统上的状态. 这意味着系统 $X$ 的状态应该由 $\vec{p} \in \mathbb{R}^n$ 来表述, 其中 $n = \abs{\Gamma_X}$ 是状态集的大小. 这样的概率是一个概率向量 $\vec{p}$, 满足 $\sum_i p_i = 1$, $\vec{p} \geq \vec{0}$. 其中 $\vec{0}$ 代表的是所有元素都是 $0$ 的向量, 而 $\geq$ 是一个对应元素两两相比的大于等于关系. (这是不是很像量子态 $\tr[\rho] = 1$, $\rho\geq 0$ 的限制?)
我们可以看到, 一个经典信道本质上就是一个概率转移过程 $\vec{p} \to \vec{q}$. 由于我们讨论的是一个信道输入的信号与输出信号的关系, 这里我们仅关注于离散时间的随机过程. 一般而言, 源信号 $\vec{p}$ 与目标信号 $\vec{q}$ 的维度不一定相同. 但是在有限维系统中, 我们总是可以用补零的办法使它们的维度相同. 也就是说, 假设 $\vec{p} = (p_0,p_1)$, $\vec{q} = (q_0,q_1,q_2)$, 我们可以选择 $\vec{p}^\prime = (p_0,p_1,0)$, 从而让这两个概率向量的维度相同. 这就像我们规定文章中必须在段尾加空格对齐每一行的宽度. 这个行为不会增加任何的信息量, 只是让我们的格式更加整齐. 由于补零的存在, 这里我们只关心信道传输前后维度相等的情况.
信道代表着概率向量的转移过程, 这可以由概率转移矩阵 $T$ 所描述. $\vec{q} = T \vec{p}$ 在 $\vec{p}$ 为概率向量时, $\vec{q}$ 也一定要是概率向量. 即对任意的 $\vec{p}$, $\sum_i q^i = \sum_{i,j} T_j^i p^j = \sum_j p^j (\sum_i T_j^i) = 1$. 这意味着 $T$ 的每一列的和都必须为 $1$. 如果 $\vec{p}$ 与 $\vec{q}$ 的维度相同, 这样的方阵也叫随机矩阵 (Stochastic Matrix).
英语中 stochastic 与 random 是两个同义词, 意思都是随机. 但是由于历史原因, 它们在数学中表示的是不同的概念. 不要将 stochastic matrix 与 random matrix 混淆. 前者等价于概率转移矩阵, 后者的意思是这个矩阵本身是随机生成的.
优超与态转换
由于信息的交换不变性, 为了研究信息, 我们需要给信息量相同的态归入各自的等价类. 对于概率向量而言, 我们对其进行任意的排序不改变信息量. 因此, 我们规定所有的概率向量 $\vec{p}$ 需要从大到小排列: $\vec{p}^\downarrow = (p_0,p_1,\cdots, p_{n-1})$ 满足 $p_0\geq p_1 \geq \cdots\geq p_{n-1}$. 每一个这样的降序向量都唯一地表示了一个交换不变的态.
在将信息归类之后, 我们还需要将不同态的信息量进行排序. 这个排序方法应该满足
- 如果我可以在不使用额外信息的情况下, 从态 $p$ 恢复出态 $q$ 的信息, 那么 $q$ 的信息量应该不大于 $p$ 的信息量.
这就涉及了两件事情:
- 什么叫恢复?
- 什么叫不使用额外信息?
我们从态 $p$ 恢复出态 $q$ 意味着, 我们可以使用一个信道 $\Gamma$, 使得 $q = \Gamma(p)$. 然而什么叫没有额外信息就比较有争议性了. 一个简单的原则就是 “garbage in, garbage out”, 即垃圾输入则垃圾输出. 也就是说, 如果我一点信息也不输入这个信道, 那么这个信道的输出也应该一点信息也没有. 但是这就把问题引向了一个概率论中的哲学问题, 什么样的输入态叫做”没有信息”呢? 或者从贝叶斯主义的角度来说, 如果我对一个状态一无所知, 我应该假设什么样的先验概率呢?
一个经典的选择是完全混态. 即如果我们对一个系统一无所知, 那么我们认为这个系统处于任何一个可能的态的情况是等概率的. 这样的状态被称为完全混态 $\mathbb{I}/n := (\frac{1}{n},\frac{1}{n},\cdots,\frac{1}{n})$. 在这个前提下, 所谓一个信道不使用额外信息就意味着, 如果我们输入这个信道的是完全混态, 它也一定要输出完全混态. 对于这样的信道, 我们可以验证, 用于描述它的概率转移矩阵的每一行的和也都是 $1$. 这样每一行加起来是 $1$, 每一列加起来也是 $1$ 的矩阵被称为双随机矩阵.
- 优超
-
如果一个概率向量 $p$ 可以被一个双随机矩阵 $D$ 转换成 $q$, 即 $q = Dp$, 那么我们说 $p$ 优超于 $q$. 这被记做 $p \succeq q$.
然而优超的定义是存在性, 而非构造性的. 这在数学的处理上很麻烦. 有意思的是, 优超实际上与降序向量有着非常深刻的联系:
-
$p \succeq q$ 当且仅当对所有 $k$ 都有 $\sum_{i=0}^k p_i^\downarrow \geq \sum_{i=0}^k q_i^\downarrow$.
这里 $\sum_{i=0}^k p_i^\downarrow$ 即 $p$ 的最大 $k$ 项的和. 这个事实是基于 Birkhoff-von Neumann 定理的: 所有的双随机矩阵都是置换矩阵的凸组合. 这意味着 对 $q$ 的任意的索引集 $S$, $\sum_{i\in S} p_i = \sum_{\pi} a(\pi) \sum_{j \in\pi^{-1}(S)} p_j$ 这里第一个求和是对所有的转置 $\pi$, 其中概率向量 $\sum_\pi a(\pi) = 1$. 而 $\sum_{j \in\pi^{-1}(S)} p_j$ 是 $S$ 在逆转置后的索引集对应的那些 $p$ 中的元素的和.
- 每个元素的转置及逆转置的结果都是唯一的, 因此逆转置后的索引集的大小与 $S$ 是一样的;
- $q$ 是这些 $\sum_{j \in\pi^{-1}(S)} p_j$ 的凸组合, 因而 $q$ 不大于这些和中最大的那个.
因此, 必然存在一个 $\pi$ 使得 $\sum_{i\in S} q_i \leq \sum_{j\in T} p_j$, 其中 $T = \pi^{-1}(S)$. 这对所有的 $S$ 都成立, 因而对 $q$ 中最大的 $k$ 个元素的和, 也必然存在 $p$ 中的 $k$ 个元素加起来比它大. 这便得到了上述的定理1.
优超的这种等价形式给了我们一种将优超可视化的方法, 即 Lorenz 曲线:
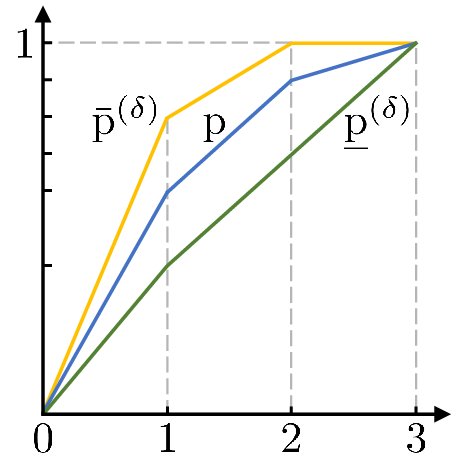
我们将 $\sum_{i=1}^k p_i^\downarrow$ 从左至右画在坐标轴上. 横轴左表是 $k$. 由于 $p^\downarrow$ 是降序的, 所以每一段曲线都比它左边的线平缓. 根据优超的等价形式, $p \succeq q$ 当且仅当 $q$ 的曲线的每一个点都比 $p$ 的曲线中每一个点要低. 只要画出 Lorenz 曲线, 我们就可以简单的通过 $p$ 是否包裹住 $q$ 来判断我们是否能通过不使用额外信息的信道将 $p$ 变成 $q$.
对于量子态而言, 由于信息是基底变换不变的, 我们总是可以通过酉变换把密度算子对角化. 这样我们可以类似地把量子态的转换过程用优超表示出来:
- Uhlmann 优超定理
-
当且仅当一个密度算子 $\rho$ 可以被保单位信道 (unital channle) 转换成 $\sigma$, $\rho$ 的谱 $\lambda(\rho)$ 优超于 $\lambda(\sigma)$. 我们把这个叫做厄米算子优超, $\rho \succeq \sigma$.
这里保单位信道的意思是如果向该信道输入完全混态, 那么输出也是完全混态. 根据 Lorenz 曲线的斜率递减的性质, 不难看出, 对角线, 即完全混态处于优超关系的最底层. 而 $(1,0,\cdots, 0)$ 处于优超关系的最顶层. 它们分别代表着完全没有信息, 以及最大信息.
偏序与熵
虽然优超很好的刻画了信息的相对关系, 但是优超是一个偏序关系. 偏序关系意味着, 如果 $p \succeq q$, 那么我们可以明确的比较它们信息量的大小, 但是存在某些概率向量 $a,b$, 有 $a \nsucceq b$ 且 $b \nsucceq a$. 我们天然的喜欢全序的关系, 即可以用数字大小来比较的关系. 这意味着我们需要一个将态关联到实数上的映射 $f$, 满足
- 如果 $a \succeq b$, 则 $f(a) \leq f(b)$ (或者反过来 $f(a) \geq f(b)$).
这样的函数 $f$ 叫舒尔凹 (凸) 函数. 我们一般习惯性的选择舒尔凹函数, $f(a) \leq f(b)$. 另外, 由于信息是置换不变的, 我们希望 $f$ 是一个相对置换对称的函数. 这样的函数一般可以被称为熵函数.
当然, 在我们具体选择熵函数的时候, 我们会加上一些额外的条件. 最一般的条件是, 如果一个概率向量的降序向量是 $(1,0,\cdots,0)$, 那么它的熵应该等于 $0$. 这一点通过给舒尔凹函数加上一个常数并不难做到. 这样的偏置并不改变舒尔凹函数的性质. 在实际工作中, 我们一般还希望熵函数是连续的.
大家常用的一般有两族熵函数: Renyi 熵与 Tsallis 熵
- Renyi 熵: $H_\alpha(p) := \frac{1}{1-\alpha} \log\qty(\sum_i p_i^\alpha)$, $\alpha \geq 0$;
- Tsallis 熵: $S_q(p) := \frac{1}{q-1}\qty(1- \sum_i p_i^q)$;
其中由于 Renyi 熵满足可加性 (即两个不相关系统的整体熵等于每个子系统各自的熵的和) 在信息论中更为常用. 实际上这两族熵函数在 $\alpha\to 1$ 或者 $q\to 1$ 的极限下都等价于香农熵. 由于香农熵良好的渐进性质, 在大多数信息论的科普文章中都会以它为开头. 根据香农信源编码定理, 香农熵代表了数据在无穷次被使用时, 压缩的极限.
系综与量子统计力学
我在前面提到, 我们定义不使用额外信息的方法是假设完全没有信息的态是完全混态. 然而贝叶斯主义告诉我们, 这并不是唯一的选择. 虽然这个选择符合我们的直觉, 但这并不意味着它就是最正确的.
如果我们选择其他的分布作为零信息的分布呢? 如果我们认为概率向量 $\tau$ 才是不包含信息的状态, 那么信息量的序关系应该被定义为使用 $\Gamma(\tau) = \tau$ 的信道时, 信息量小的系统不能被还原成信息量大的系统.
对于这样的系统, 我们把信息源记为 $(p,\tau)$. 我们定义 $\tau$-降序排列为
\[(p,\tau)^\downarrow := ((p_0,\tau_0),\cdots, (p_{n-1},\tau_{n-1}))\]使得 $\frac{p_k}{\tau_k} \geq \frac{p_{k+1}}{\tau_{k+1}}$. 这里我们要求 $\tau_i$ 皆严格大于 $0$. 可以看到, 如果 $\tau = \mathbb{I}/n$ 是完全混态, 这个 $\tau$-降序排列等价于 $p$ 的降序排列.
- d-优超
-
如果一对概率向量 $(p,\tau)$ 可以被一个随机矩阵 $T$ 转换成 $(q,\tau^\prime)$, 即 $q = Tp$; $\tau^\prime = T\tau$, 那么我们说 $(p,\tau)$ 优超于 $(q,\tau^\prime)$. 这被记做 $(p,\tau) \succeq (q,\tau^\prime)$.
根据 $\tau$-降序关系, 我们同样可以画出 Lorenz 曲线
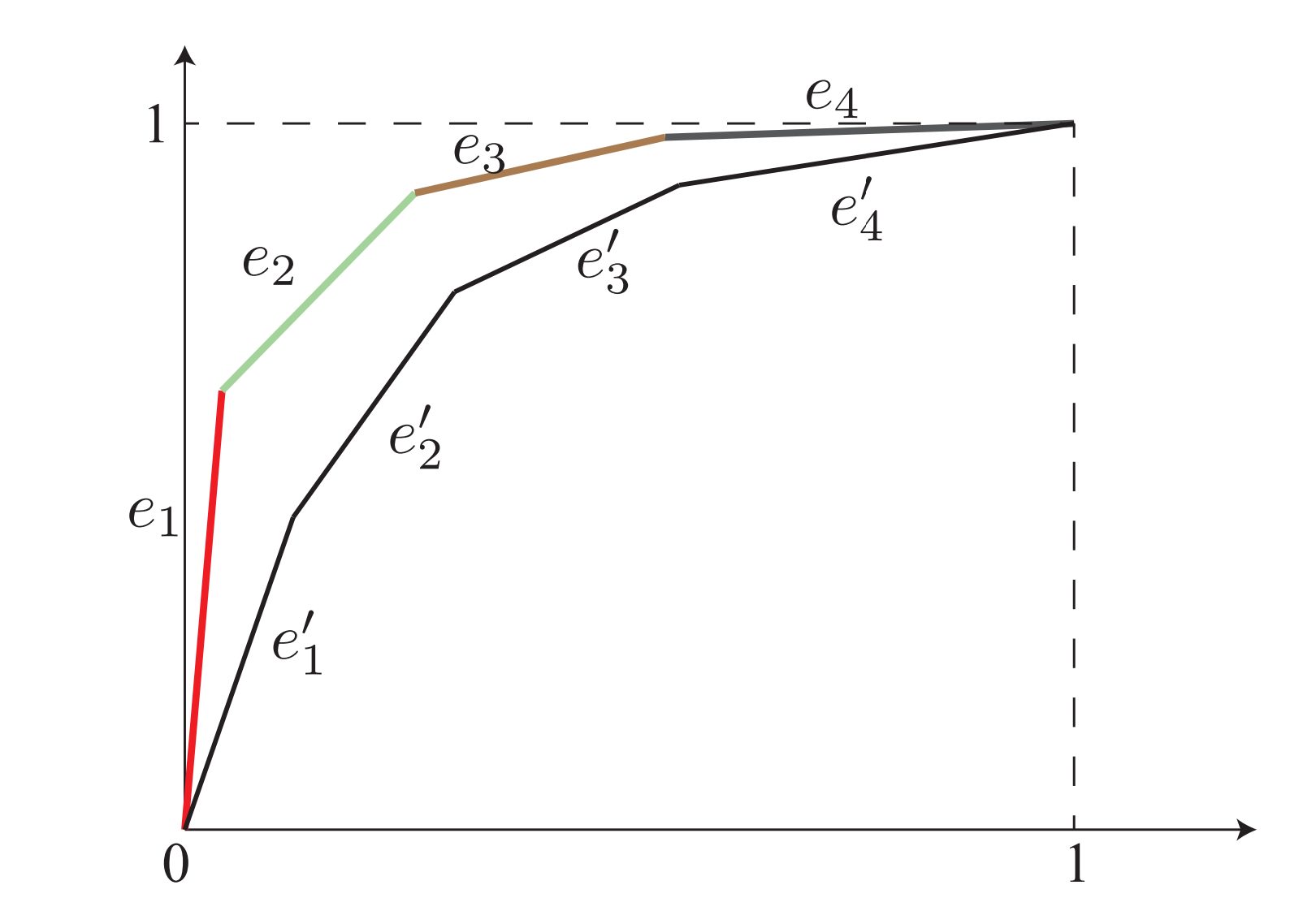
其中每个节点的坐标为 $(\sum_{i=1}^{k} p_i, \sum_{i=1}^k \tau_i)$. 这个序列中每一个点 $(x,y)$ 的斜率都要比前一个要小. 有意思的是, d-优超同样满足 Lorenz 曲线与态转化之间的关系. 也就是说
-
当且仅当 $(p,\tau)$ 的 Lorenz 曲线包裹住 $(q,\tau^\prime)$, 有 $(p,\tau) \succeq (q,\tau^\prime)$.
由于 Lorenz 曲线的函数 $f$ 可以被表示为2
\[f(x) = \max_{c_i\leq 1: x=\sum_i c_i \tau_i} \sum_i c_i p_i \ ,\]如果我们将取到 $f$ 最大值的那些 $c_i$ 记为 $c_i^\ast$, 假设存在满足优超的随机矩阵 $T$, 我们有
\[f^\prime(x) = \sum_i c^\ast_i q_i = \sum_{i,j} c_i^\ast T_{i,j} p_j \ ,\]而根据 $c^\ast$ 的定义,
\[x = \sum_i c^\ast_i \tau^\prime_i = \sum_{i,j} c_i^\ast T_{i,j} \tau_j \ .\]记 $\sum_i c^\ast_i T_{i,j}$ 为 $d_j$, 则
\[f^\prime(x) = \sum_j d_j p_j \leq \max_{d_j\leq 1: x=\sum_j d_j \tau_j} \sum_j d_j p_j = f(x)\]由于 $T$ 是随机矩阵, $d_j \leq 1$, 因此不等式左边的 $d_j$ 的取值在右边的可行集范围内. 根据最大值的定义, 左边不大于右边, 即对所有 $x$ 都有 $f^\prime(x) \leq f(x)$. 即整个 $f^\prime$ 曲线都在 $f$ 曲线下方.
有意思的是, 这个性质与系综理论有着很深的联系. 在 $\tau^\prime = \tau$ 的情况下, 我们可以用指数 $\frac{e^{-\beta \epsilon_i}}{Z}:= \tau_i$ 来替代概率向量. 这里 $Z = \sum_i e^{-\beta \epsilon_i}$ 被称为配分函数, . 对于有限大的 $\epsilon_i$, 显然 $\tau_i$ 是一个严格大于零的数. 也就是说, 对于有限的向量 $(\epsilon_1, \epsilon_2,\cdots, \epsilon_n)$, 其对应的 $\tau$ 一定可以用来定义 $\tau$-降序排列.
对于有限维的厄米算子 $H$, 它的谱可以被看作如上的 $\epsilon_i$ 向量. 此时 $\tau$ 即为 $\frac{e^{-\beta H}}{\tr[e^{-\beta H}]}$ 的谱. 这个指数态被称为 Gibbs 态, 或者按统计物理传统叫它 Gibbs 正则系综. 但是在量子信息中系综有特殊的含义, 因而我们更习惯于叫它 Gibbs 态. 从物理的角度来看 $\beta$ 正比于热力学温标的倒数, Gibbs 态被理解为热态. 也就是说, 对于一个处于 Gibbs 正则系综内的物体, 在进入热力学平衡态之后, 它一定处于 Gibbs 态. 在这个背景下, 当我们对一个系统一无所知的时候, 似乎 Gibbs 态而非完全混态更像一种”不带有信息”的态. 实际上 d-优超就是一种刻画系统与热力学平衡态的距离的一种度量.
根据 d-优超的性质, 当且仅当一个态 $\rho$ 可以被一个保证 Gibbs 态不变的信道 $\Gamma$ 转化成 $\sigma$ 时, $(\lambda(\rho),\tau) \succeq (\lambda(\sigma),\tau)$. 这里 $\lambda$ 代表着算子的谱. 满足这样的性质的信道叫保 Gibbs 信道. 但是量子统计力学的复杂性在于, 保 Gibbs 信道并没有考虑能量的消耗, 但是统计力学关心的是热机的性质, 即热态与能量的交换比. 为了讨论这种交换比, 我们只能使用热操作 (thermal operation). 可以证明所有的热操作都是保 Gibbs 信道, 但是反过来就不是了. 这二者之间的细节差别也是量子统计力学的复杂之所在.
数据处理不等式
更一般地, 我们在信息论中希望讨论所有信道的性质. 对所有信道都可以定义的信息损失的不可逆性质可以由数据处理不等式给出. 经典(强)信息处理不等式有 $3$ 种形式:
- 任意两个概率向量的总变差 (total variation) $\sup_S \abs{p(S) - q(S)}$ 在经过任意信道后不会增加;
- 任意两个概率向量的相对熵/KL-散度 $ \sum_i p_i \log\frac{p_i}{q_i}$ 在经过任意信道后不会增加;
- 对于任意的马尔可夫链 $X \to Y \to Z$, 互信息 $I(X,Y) \geq I(X,Z)$;
其中互信息的定义为 $I(X,Y):= H(X) + H(Y) - H(X,Y)$, 即各个子系统的熵的和减去整个系统的熵. 它们本质上是等价的3.
这三种经典形式都可以直接推广为量子数据处理不等式:
- 任意两个密度算子的迹距离 $\sup_{\mathbb{I}\geq P\geq0}\tr[P(\rho-\sigma)]$ 在经过任意量子信道后不会增加;
- 任意两个概率向量的 von Neumann 相对熵 $D(\rho\Vert \sigma):=\tr[\rho \log\rho - \rho\log \sigma]$ 在经过任意量子信道后不会增加;
- 对于任意的量子马尔可夫过程 $X \to Y \to Z$, 量子互信息 $I(X,Y) \geq I(X,Z)$;
这三个量在密度算子是对角算子时, 都分别可以被归约为上面三个经典度量. 这里前两个度量当且仅当两个态相同时为 $0$, 而互信息 $I(X,X) = H(X)$.
我们这里就不是在讨论一个态与完全未知态之间的距离, 而是给了一个参考系统. 即数据处理不等式告诉我们两个不同的状态在经过同一个信道后只会更加不可分. 这从另外的角度描述了什么是信息的损失. 由于这个定义不涉及具体的参考态, 因而可以被用于所有的信道.
- 对于信道 $\Gamma$, 前两个形式实际上就是在说在 $\Gamma(\sigma) = \sigma^\prime$ 的前提下, $\rho^\prime$ 只能更接近 $\sigma^\prime$. 如果信道输入与输出系统维度相同, 这就是一种 d-优超.
- 如果把 KL-散度的参考态 $\tau$ 换成完全混态, 那么这个散度就等于 $H(\rho)-d$. 这实际上是把基于系综的信息处理不等式退化成了第三节中讨论的朴素信息熵的不等式.
- 而第三种形式可以被理解为, $X$ 系统被做了一个备份 (对应量子系统而言, 就是处于最大纠缠态). 第一个马尔可夫过程把其中一个 $X$ 系统转换成了 $Y$, 制备了一个关联起 $X,Y$ 两个系统的状态. 当我们在 $Y$ 系统上再作用一个信道, 这个互信息关系意味着输出的系统更接近于可分态. 事实上我们有 $I(X:Y) = D(\rho^{X,Y}\Vert \rho^X\otimes \rho^Y)$, 这里 $D$ 代表着 KL-散度.
Ref:
-
Watrous, John. The theory of quantum information. Cambridge university press, 2018.Infomation ↩
-
Shiraishi, Naoto. “Two constructive proofs on d-majorization and thermo-majorization.” Journal of Physics A: Mathematical and Theoretical 53.42 (2020): 425301. ↩
-
Polyanskiy, Yury, and Yihong Wu. “Strong data-processing inequalities for channels and Bayesian networks.” Convexity and Concentration. Springer, New York, NY, 2017. 211-249. ↩